import java.util.Arrays;
import java.util.Scanner;
public class FjuMap {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int startVertex;
int endVertex;
String[] names = {"利瑪竇大樓", "伯達樓", "樹德樓", "羅耀拉大樓", "濟時樓", "仁愛學苑", "聖心學苑", "信義/和平學苑/心園", "法園(社會服務中心)/仁園", "創新育成中心"};
int[][] path = new int[10][10];
int[][] graph =
{{0, 13, Integer.MAX_VALUE, 25, Integer.MAX_VALUE, 27, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE},
{13, 0, 10 , 20, Integer.MAX_VALUE, 35, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE},
{Integer.MAX_VALUE, 10, 0, 12, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE},
{25, 20, 12, 0, 20, 22, Integer.MAX_VALUE, 28, 27, Integer.MAX_VALUE},
{Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 20, 0, 25, Integer.MAX_VALUE, Integer.MAX_VALUE, 16, Integer.MAX_VALUE},
{27, 35, Integer.MAX_VALUE, 22, 25, 0, 9, 9, Integer.MAX_VALUE, Integer.MAX_VALUE},
{Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 9, 0, 8, Integer.MAX_VALUE, Integer.MAX_VALUE},
{Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 28, Integer.MAX_VALUE, 9, 8, 0, 10, 12},
{Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 27, 16, Integer.MAX_VALUE, Integer.MAX_VALUE, 10, 0, 7},
{Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 12, 7, 0}};
for (int[] i: path)
Arrays.fill(i, -1);
for (int i=0; i<graph.length; i++) {
for (int j=0; j<graph.length; j++) {
for (int k=0; k<graph.length; k++) {
if (!(graph[i][k] == Integer.MAX_VALUE) && !(graph[k][j] == Integer.MAX_VALUE)) {
int newWeight = graph[i][k] + graph[k][j];
if (newWeight < graph[i][j]) {
graph[i][j] = newWeight;
path[i][j] = k;
}
}
}
}
}
System.out.println("地點清單:");
System.out.println("-----------------------");
for (int i=0; i<names.length; i++)
System.out.println(i + "." + names[i]);
System.out.println("-----------------------");
try {
while (true) {
System.out.print("請輸入起點編號(輸入10結束):");
startVertex = sc.nextInt();
if (startVertex == 10)
break;
System.out.print("請輸入終點編號:");
endVertex = sc.nextInt();
System.out.print("最短路徑:");
System.out.print(names[startVertex]);
tracePath(path, names, startVertex, endVertex);
System.out.println("->" + names[endVertex] + "\n");
}
} finally {
sc.close();
}
}
private static void tracePath(int[][] path, String[] names, int startVertex, int endVertex) {
if (path[startVertex][endVertex] != -1) {
tracePath(path, names, startVertex, path[startVertex][endVertex]);
System.out.print("->" + names[path[startVertex][endVertex]]);
tracePath(path, names, path[startVertex][endVertex], endVertex);
}
}
}
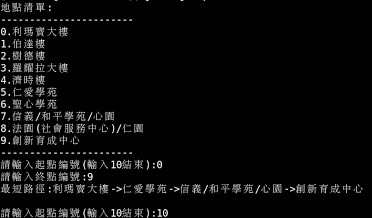
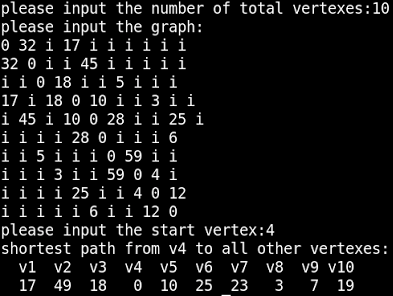
範例輸入輸出:
抱歉沒空說明程式碼,只能說明一下輸入輸出的部份。首先依照地點清單輸入起點編號,再輸入終點編號,程式就會印出最短路徑,若在起點編號那裡輸入10,程式就會結束。