Dijkstra's Algorithm

Java code:

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Scanner;
import java.util.Set;

public class DijkstraAlgorithm {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int vertexNum;
        Set<Integer> used = new HashSet<Integer>();
        Map<Integer, Map<Integer, Integer>> graph = new HashMap<Integer, Map<Integer, Integer>>();
        Map<Integer, Integer> shortestPath = new HashMap<Integer, Integer>();
        int startVertex;
        
        try {
            System.out.print("please input the number of total vertexes:");
            vertexNum = sc.nextInt();
            System.out.println("please input the graph:");
            for (int i=1; i<=vertexNum; i++)
                graph.put(i, new HashMap<Integer, Integer>());
            for (int i=1; i<=vertexNum; i++) {
                for (int j=1; j<=vertexNum; j++) {
                    String input = sc.next();
                    
                    if (input.equals("i"))
                        graph.get(i).put(j, Integer.MAX_VALUE);
                    else
                        graph.get(i).put(j, Integer.parseInt(input));
                }
            }
            System.out.print("please input the start vertex:");
            startVertex = sc.nextInt();
        } finally {
            sc.close();
        }
        for (int i=1; i<=vertexNum; i++)
            shortestPath.put(i, graph.get(startVertex).get(i));
        used.add(startVertex);
        while (true) {
            int nearestVertex = -1;
            int smallestWeight = Integer.MAX_VALUE;
            
            for (int i=1; i<=vertexNum; i++) {
                if (!used.contains(i) && shortestPath.get(i) < smallestWeight) {
                    nearestVertex = i;
                    smallestWeight = shortestPath.get(i);
                }
            }
            used.add(nearestVertex);
            if (used.size() == vertexNum)
                break;
            for (int i=1; i<=vertexNum; i++) {
                if (graph.get(nearestVertex).get(i) != 0 && graph.get(nearestVertex).get(i) != Integer.MAX_VALUE) {
                    int newPath = shortestPath.get(nearestVertex) + graph.get(nearestVertex).get(i);
                    
                    if (newPath < shortestPath.get(i))
                        shortestPath.put(i, newPath);
                }
            }
        }
        System.out.println("shortest path from v" + startVertex + " to all other vertexes:");
        for (int i=1; i<=vertexNum; i++)
            System.out.printf("%4s", "v" + i);
        System.out.println();
        for (int i=1; i<=vertexNum; i++)
            System.out.printf("%4d", shortestPath.get(i));
        System.out.println();
    }
}

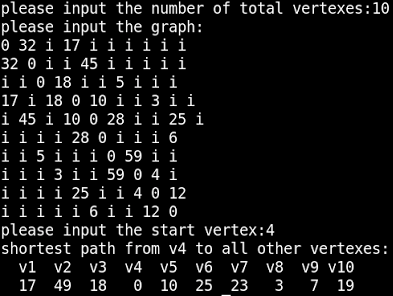
範例輸入輸出:

---

抱歉沒空說明程式碼，只能說明一下輸入輸出的部份。首先輸入圖形上總共點的數量，再輸入相鄰矩陣，橫軸表示點1~點10，縱軸也是表示點1~點10，輸入的是點到點之間的權重，若輸入i表示這兩點不相連，也就是權重無限大，最後再輸入以哪個點當作起點，程式會找出由這個點到其他所有點的最短距離。輸出結果表示由出發點到各點的距離。本範例輸入是採用課本習題2的圖，所以可以參照課本的圖方便了解。